Waveform Generation Functions

This page contains some code for generating different audio waveforms. They are written in c, but could be easily translated to other languages.

An archive containing the source code for creating all the samples is link to below.

Simply unpack and make the files as shown below.

> unzip wavGen.zip
> cd wavGen
> make
> ./wavGen

This will produce four 10 second wav files; A simple tone at 440Hz, a logarithmic sweep from 110Hz to 1760Hz, and two white noise files, one based on the rand() function, the other based on the Mersenne Twister. Each wav file is fade-in and fade-out of 0.25 seconds.

Simple Test Tone

Really very simple, but here basically for lazy cut n' pasting.

void genTone(float *buffer, long numSamples, int sampleRate, float freq)
{
   long s;
   for (s=0 ; s<numSamples ; s++) buffer[s] = sin(2.0 * M_PI * freq * s / sampleRate);
}

Frequency Sweep

This function generates a logarithmic frequency sweep. It is based on a Matlab function by Jez Wells.

void genSweep(float *buffer, long numSamples, int sampleRate, float minFreq, float maxFreq)
{
   double start = 2.0 * M_PI * minFreq;
   double stop = 2.0 * M_PI * maxFreq;
   double tmp1 = log(stop/start);

   long s;
   for (s=0 ; s<numSamples ; s++) {
      double t = (double)s / numSamples;
      double tmp2 = exp(t * tmp1) - 1.0;
      buffer[s] = sin( (start*numSamples*tmp2) / (sampleRate*tmp1) );
   }
}

White Noise

White noise can be generated using a random number generator. However, the flatness of the output's spectrum depends on how good the random number generator is. Two functions are shown below, the first uses the rand() function. The second uses the well known Mersenne Twister. The advantage of this latter approach is that you have control over how the random numbers are generated, whereas the implementation of rand() may vary between system libraries.

void genWhiteNoise(float *buffer, long numSamples)
{
   float div = (float)RAND_MAX / 2.0f;
   while (numSamples--) buffer[numSamples] = (rand() / div) - 1.0f;
}

int main(void)
{
   ...
   init_genrand(time(0));
   ...
}

void genWhiteNoise_twist(float *buffer, long numSamples)
{
   while (numSamples--) buffer[numSamples] = (2.0 * genrand_real1()) - 1.0;
}

Fade In and Out

Fading each end of the wave avoids the chance of any nasty clicks at the start and end of playback. As shown in the images below it is simply a case of applying an envelope at each end of the waveform.

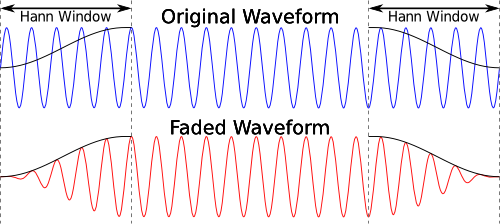
In this case the envelope is generated using half of a Hann Window. The equation is shown below. In this case, numSamples is the number of samples over which to apply the envelope.

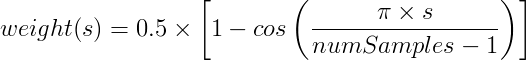
A function that applies the envelope to each end of a buffer of samples is shown below.

void fadeInOut(float *buffer, long numSamples, int sampleRate, float fadeTime)
{
   // Calculate duration, in samples, of fade time
   long numFadeSamples = fadeTime * sampleRate;

   // Make sure the fade time is not longer than the number of avialable samples
   if (numFadeSamples > numSamples) numFadeSamples = numSamples;

   long s;
   for (s=0 ; s<numFadeSamples ; s++)
   {
      // Calculate weight based on Hann 'raised cosine' window
      float weight = 0.5 * (1 - cos(M_PI * s / (numFadeSamples - 1)));

      // Apply weighting
      buffer[s] *= weight;                      // Fade In
      buffer[numSamples-(s+1)] *= weight;       // Fade Out
   }
}